2.1. Población, muestra, individuo y carácter
Recordamos de forma rápida los conceptos de población, muestra, individuo y carácter.
- Población: Conjunto o colección de objetos al que está referido un estudio estadístico. El vocablo suena a personas pero una población estadística puede estar constituida por cualquier tipo de elemento, es decir, una población puede estar constituida por personas pero también por objetos de cualquier tipo de naturaleza. Por ejemplo, en un estudio sobre la incidencia de cierta enfermedad en un país, la población sería todos los habitantes de dicho país. En un estudio sobre la calidad de la producción de ciertos componentes para ordenadores, la población serían todos los componentes que se han fabricado.
- Individuo: Cada uno de los elementos que forman parte de la población. En sentido estadístico un individuo al igual que ocurre para el concepto de población, puede ser algo con existencia real, como una peersona, un automóvil o una casa, o algo más abstracto como la temperatura, una opinión, un voto o un sentimiento.
- Carácter: Cualquier carácterística o propiedad que pueda ser estudiada en todos los elementos de la población. Así por ejemplo si consideramos como elemento a una persona, podemos distinguir en ella multitud de caracteres como el sexo, la edad, estatura, peso, color de pelo, nivel de estudios, etc.
- Muestra: Cualquier subconjunto de una población. Cuando los elementos que componen la muestra están elegidos aleatoriamente y todos los elementos tienen la misma probabilidad de ser elegidos diremos que se trata de una muestra aleatoria simple. Por norma general, en un estudio estadístico hay muchos condicionantes de tipo económico, físico, o de otro tipo que impiden trabajar con todos los elementos de la población, por tanto, se suele recurrir a muestras representativas de la población. Los procedimientos a seguir para la elección de este tipo de muestras se estudian en una parte de la Estadística Inferenciasl que se denomina muestreo.
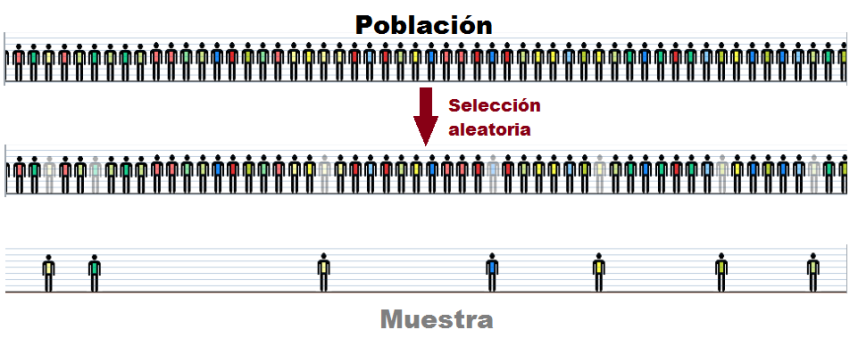
En la siguiente escena puedes observar cómo se puede realizar la elección de muestras representativas de una determinada población. Puedes realizar varias pruebas y extraer tus propias conclusiones.
Escena desarrollada por José Ireno Fernández Rubio(RED Descartes)
2.2. Caracteres y tipos de caracteres
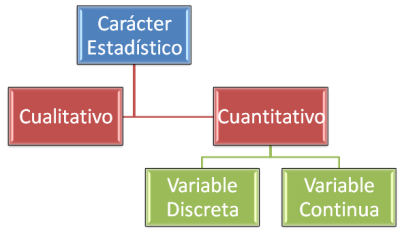
Toda propiedad o característica que pueda estudiarse en los elementos de una población se denomina carácter estadístico. La primera gan diferenciación de una característica es que se pueda medir mediante un número o que no se pueda. En este sentido distinguimos:
- Carácter cualitativo o Atributo. Los atributos son aquellos caracteres que no pueden ser descritos numéricamente, al menos en principio. Para su descripción por tanto utilizamos la palabra, el sustantivo, adjetivo y adverbio fundamentalmente. Por ejemplo: Sexo profesión, estado civil, color de ojos, color de pelo, nacionalidad, etc. A su vez se pueden clasificar en:
- Ordenables: Aquellas que sugieren una ordenación o son susceptibles de ella, por ejemplo la graduación militar, El nivel de estudios, grado de satisfacción, etc.<
- No ordenables: Aquellas que sólo admiten una mera ordenación alfabética, pero no establece orden por su naturaleza, por ejemplo el color de pelo, sexo, estado civil, entre otros.
- Variables Cuantitativas. Son las que pueden ser descritas por medio de números. Dentro de éstas a su vez se pueden destacar:
- Cuantitativas discretas: Aquellas a las que se les puede asociar un número entero, es decir, aquellas que por su naturaleza no admiten un fraccionamiento de la unidad, por ejemplo número de hermanos, páginas de un libro, etc.
- Cuantitativas continuas: Aquellas que no se pueden expresar solamente mediante un número entero, es decir, aquellas que por su naturaleza admiten que entre dos valores cualesquiera la variable pueda tomar cualquier valor intermedio, por ejemplo peso o tiempo.
No obstante en muchos casos el tratamiento estadístico hace que variables discretas sean tratadas como si fuesen continuas. Esto ocurre por ejemplo en casos en los que la variable toma un gran número distinto de valores enteros.
En la siguiente escena puedes clasificar varios ejemplos de variable estadística y atributos. Completa todas las preguntas y afianza el concepto.
Escena desarrollada por José Ireno Fernández Rubio(RED Descartes)
En esta escena puedes practicar con ejercicios de clasificación de variables según los distintos tipos. la escena plantea ejercicios de clasificación de forma aleatoria. Realiza varios ejemplos hasta comprobar que no cometes errores.
Escena desarrollada por Juan Jesús Cañas Escamilla(RED Descartes)
- ¿Cómo hallarías el rango?
Media, moda, mediana, rango
Octavo básico - Actividad Nº 790
1- Media aritmética
La media aritmética es la suma de todos los datos dividida entre el número total de datos. Se calculan dependiendo de cómo vengan ordenados los datos.
Ejemplo:
¿Cuál es la media de las edades de Andrea y sus primos?
La media aritmética de un grupo de datos se calcula así:
Se debe multiplicar cada dato con su respectiva frecuencia, sumar todos estos productos, y el resultado dividirlo por la suma de los datos.
Ejemplo:
Se ha anotado el número de hermanos que tiene un grupo de amigos. Los datos obtenidos son los siguientes:
Hermanos: 1, 1, 1, 1, 2, 2, 2, 3, 3, 4
Si hacemos el recuento de los datos y seguimos los pasos anteriormente descritos, tenemos:
2- Moda
La moda de un conjunto de datos es el dato que más veces se repite, es decir, aquel que tiene mayor frecuencia absoluta. Se denota por Mo. En caso de existir dos valores de la variable que tengan la mayor frecuencia absoluta, habría dos modas. Si no se repite ningún valor, no existe moda.
- Ejemplo1:
¿Cuál es el dato que más se repite en el ejemplo anterior?
El dato que más se repite es el 1, es el que tiene mayor frecuencia absoluta (4 veces).
La moda del número de hermanos es 1
- Ejemplo 2:
2, 3, 4, 5 , 6 , 9
En este conjunto de datos no existe ningún valor que se repita, por lo tanto, este conjunto de valores no tiene moda.
- Ejemplo 3:
1, 1, 1, 4, 4, 5, 5, 5, 7, 8, 9, 9, 9 Mo= 1, 5, 9
Si en un grupo hay dos o varias puntuaciones con la misma frecuencia y esa frecuencia es la máxima, la distribución es bimodal o multimodal, es decir, tiene varias modas.
- Ejemplo 4:
0, 1, 3, 3, 5, 5, 7, 8 Mo = 4
Si dos puntuaciones adyacentes tienen la frecuencia máxima, la moda es el promedio de las dos puntuaciones adyacentes.
3- La mediana
La mediana es el valor que ocupa el lugar central entre todos los valores del conjunto de datos, cuando estos están ordenados en forma creciente o decreciente.
La mediana se representa por Me.
Calculo de la mediana:
1° Ordenamos los datos de menor a mayor.
- La mediana de un conjunto con un número impar de datos es, una vez ordenados los datos, el dato que ocupa el lugar central.
Ejemplo:
Calcular la mediana del conjunto de datos:
- También podemos usar la siguiente fórmula para determinar la posición del dato central:
(n + 1) /2 = mediana datos impares.
- La mediana de un conjunto con un número par de datos es, una vez ordenados, la media de los dos datos centrales.
Ejemplo:
Calcular la mediana del conjunto de datos:
4- Rango
El rango da la idea de proximidad de los datos a la media. Se calcula restando el dato menor al dato mayor.
Este dato permite obtener una idea de la dispersión de los datos, cuanto mayor es el rango, más dispersos están los datos de un conjunto.
Ejemplo:
Se preguntó a 9 familias cuántas bicicletas tenían en total, dieron las respuestas ordenadas en la siguiente tabla:
- ¿Cómo hallarías el rango?
Se resta el dato mayor al dato menor: 3 - 0 = 3; Por lo tanto el rango sería 3 en este caso.
Si el conjunto de datos que se recolecta es muy numeroso, o bien, si el rango es muy amplio, es conveniente agruparlos y ordenarlos en intervalos o clases.
La amplitud o tamaño de cada intervalo se puede calcular dividiendo el valor del rango por la cantidad de intervalos que se desean obtener.
4- Ejercicios:
1- Se le pregunta a un grupo de personas acerca de la cantidad de libros que leyó durante el año 2015, y las respuestas son: 4; 3; 2; 7; 10; 8; 2; 9; 3; 6; 8; 1; 1; 9; 2. La moda de la muestra es:
a) 2 b) 3 c) 4 d) 5 e) 9
2- Halla la mediana de las siguientes series estadísticas.
a) 1, 7, 3, 2, 4, 6, 2, 5, 6
b) 4, 2, 1, 3, 8, 5, 3, 1, 6, 7
3- Se tienen dos distribuciones cuyos datos son los siguientes:
Distribución A: 9, 5, 3, 2, 1, 2, 6, 4, 9, 8, 1, 3, 5, 4, 2, 6, 3, 2, 5, 6, 7
Distribución B: 1, 1, 3, 2, 5, 6, 7, 2, 5, 4, 3, 1, 2, 1, 5, 7, 8, 9, 9, 2, 1
a) Halla el rango de ambas distribuciones.
4- Se tiene el siguiente conjunto de datos:
10, 13, 4, 7, 8, 11, 10, 16, 18, 12, 3, 6, 9, 9, 4, 13, 20, 7, 5, 10, 17, 10, 16, 14, 8, 18
a) Obtén la mediana
Respuestas:
1- a
2- a) 1, 2, 2, 3, 4, 5, 6, 6, 7 M = 4
b) 1, 1, 2, 3, 3, 4, 5, 6, 7, 8; La mediana es la media aritmética de los dos valores centrales, M = 3,5.
3- Rango de A: 9 - 1 = 8
Rango de B: 9 - 1 = 8
4- a) Ordenamos los datos de menor a mayor:
3, 4, 4, 5, 6, 7, 7, 8, 8, 9, 9, 10, 10, 10, 10, 11, 12, 13, 13, 14, 16, 16, 17, 18, 18, 20
Como hay 26 valores, la mediana es la media de los dos valores centrales: M= 10 + 10 / 2 = 10
Arquitecto especialista en gestion de proyectos si necesitas desarrollar algun proyecto arquitectonico en Bogota contacteme en el 3006825874 o visita mi pagina en www.arquitectobogota.tk
0 comentarios:
Publicar un comentario